Function Expression :
\[f(x)=\frac{1}{2}x-\frac{1}{2}(x+1 )e^{-2x} \]Domain
\[]-\infty ;+\infty [ \]Limits
\[\lim_{x \rightarrow-\infty}f(x) = +\infty \]\[\lim_{x \rightarrow+\infty}f(x) = +\infty \]
\[ \]
Derivate
\[f^{\,\prime}(x)=- 2 \left(- \frac{x}{2} - \frac{1}{2}\right) e^{- 2 x} + \frac{1}{2} - \frac{e^{- 2 x}}{2} \]\[f^{\,\prime}(x)=\frac{\left(2 x + e^{2 x} + 1\right) e^{- 2 x}}{2} \]
\[ \]
Integral
\[F(x) = \frac{x^{2}}{4} + \frac{\left(2 x + 3\right) e^{- 2 x}}{8} \]Sign Table
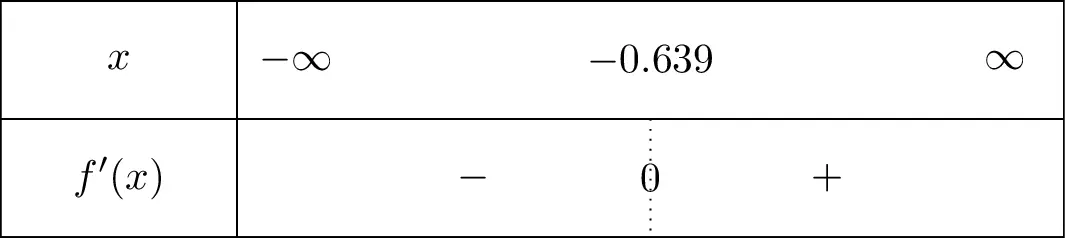
Variation Table
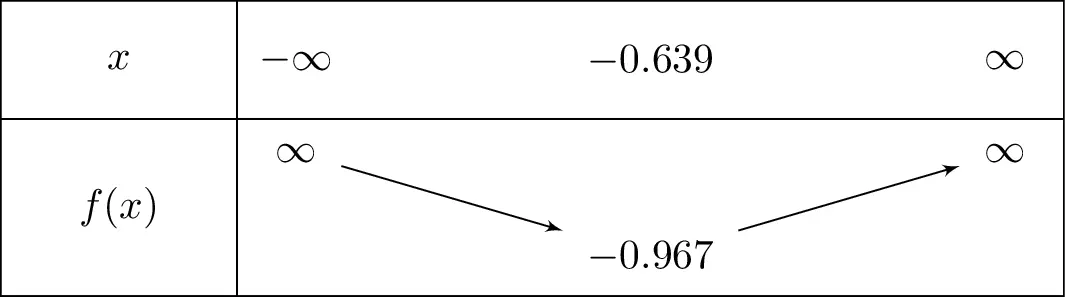
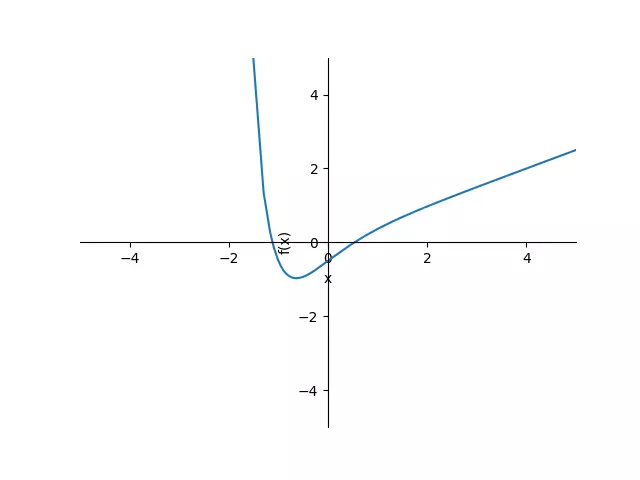
Plot
Elapsed Time: 0.0053 seconds