Function Expression :
\[f(x)=\frac{e^{-x}-1}{\frac{sin2x}{cos2x}} \]Domain
\[\mathbb{R} \setminus \left]\left\{n \pi\; \middle|\; n \in \mathbb{Z}\right\} \cup \left\{n \pi + \frac{\pi}{2}\; \middle|\; n \in \mathbb{Z}\right\} \cup \left\{n \pi + \frac{\pi}{4}\; \middle|\; n \in \mathbb{Z}\right\} \cup \left\{n \pi + \frac{3 \pi}{4}\; \middle|\; n \in \mathbb{Z}\right\}\right[ \]Limits
\[ \]Derivate
\[ \]Integral
\[F(x) = - \int \frac{\cos{\left(2 x \right)}}{\sin{\left(2 x \right)}}\, dx - \int \left(- \frac{e^{- x} \cos{\left(2 x \right)}}{\sin{\left(2 x \right)}}\right)\, dx \]Sign Table

Variation Table

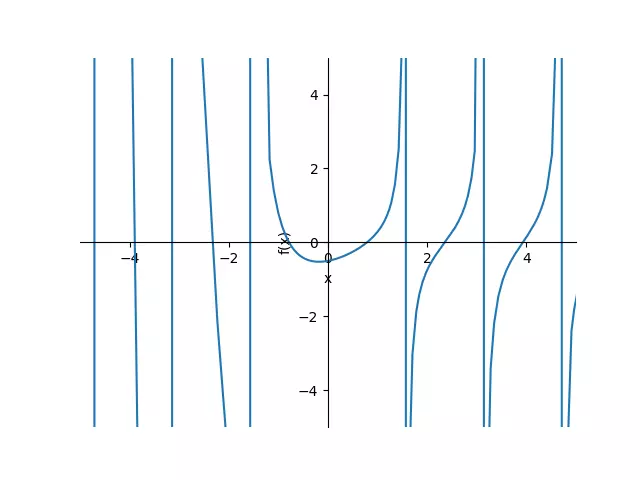
Plot
Elapsed Time: 0.0033 seconds