Exploring Prime Numbers
Prime numbers are among the most fundamental objects in mathematics, with properties and patterns that have fascinated mathematicians for centuries.
published : 19 March 2024
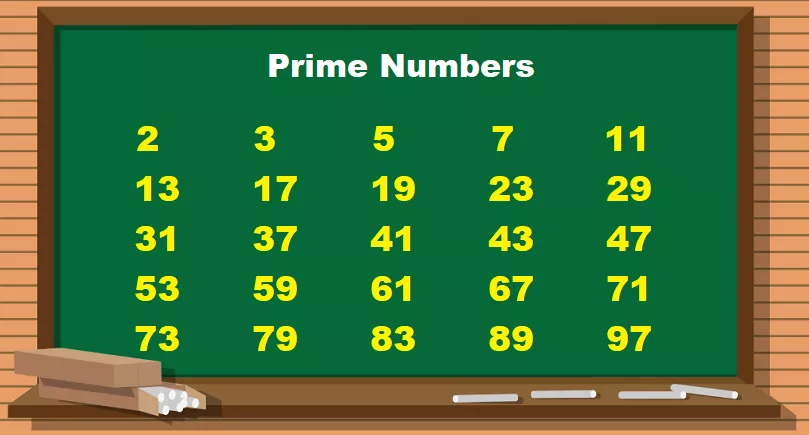
Prime numbers are among the most fundamental objects in mathematics, with properties and patterns that have fascinated mathematicians for centuries. From their role in encryption and cryptography to their applications in number theory and beyond, prime numbers continue to captivate the imagination of mathematicians and laypeople alike.
Definition and Properties
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In other words, a prime number is only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, and so on.
Prime numbers have several interesting properties, including:
- Uniqueness of Prime Factorization: Every integer greater than 1 can be uniquely expressed as a product of prime numbers, up to the order of the factors.
- Euclid's Theorem: There are infinitely many prime numbers. This theorem, proved by the ancient Greek mathematician Euclid, is one of the oldest results in number theory.
- Goldbach's Conjecture: Every even integer greater than 2 can be expressed as the sum of two prime numbers. Despite extensive computational efforts, this conjecture remains unproven.
Applications
Prime numbers play a crucial role in various areas of mathematics, science, and technology. In cryptography, prime numbers are used to generate secure encryption keys and protect sensitive information. The security of many cryptographic algorithms, such as RSA, relies on the difficulty of factoring large composite numbers into their prime factors.
Prime numbers also have applications in computer science, where they are used in algorithms for generating random numbers, testing for primality, and optimizing performance. In mathematics, prime numbers are central to many areas of number theory, including the study of congruences, Diophantine equations, and arithmetic functions.
Open Problems
Despite centuries of study, many questions about prime numbers remain unanswered. Some of the most famous open problems in number theory revolve around prime numbers, including:
- Riemann Hypothesis: The Riemann Hypothesis, one of the most famous unsolved problems in mathematics, concerns the distribution of prime numbers along the complex plane.
- Twin Prime Conjecture: The Twin Prime Conjecture posits that there are infinitely many pairs of prime numbers that differ by 2, such as (3, 5), (11, 13), and (17, 19).
- Goldbach's Conjecture: As mentioned earlier, Goldbach's Conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers.
Conclusion
Prime numbers are not only mathematical objects of beauty and intrigue but also fundamental building blocks of number theory and modern cryptography. Their properties and patterns continue to challenge and inspire mathematicians, driving advances in mathematical research and technological innovation.
As we continue to explore the mysteries of prime numbers and their applications, let us marvel at the elegance and complexity of these fundamental objects and appreciate their profound significance in the world of mathematics and beyond.