Exploring the Riemann Hypothesis
The Riemann Hypothesis is one of the most famous and longstanding unsolved problems in mathematics.
published : 10 April 2024
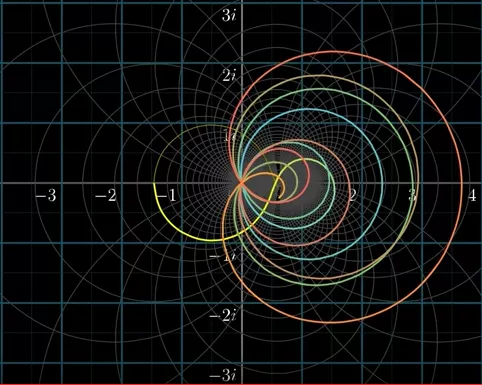
The Riemann Hypothesis is one of the most famous and longstanding unsolved problems in mathematics, with implications that extend far beyond the realm of number theory. Proposed by German mathematician Bernhard Riemann in 1859, the Riemann Hypothesis is a conjecture about the distribution of prime numbers and the zeros of the Riemann zeta function.
Riemann Zeta Function
The Riemann zeta function, denoted by ζ(s), is a mathematical function that plays a central role in number theory and has connections to various areas of mathematics, including analysis, geometry, and physics. The Riemann zeta function is defined for complex numbers s with real part greater than 1 by the infinite series:
ζ(s) = 1s + 2s + 3s + 4s + ...
One of the key properties of the Riemann zeta function is its relationship to the distribution of prime numbers. The Riemann Hypothesis conjectures that all non-trivial zeros of the Riemann zeta function lie on the critical line in the complex plane with real part equal to 1/2.
Significance and Consequences
The Riemann Hypothesis has profound implications for the distribution of prime numbers and the structure of the number system. If proven true, the Riemann Hypothesis would provide deep insights into the behavior of prime numbers and establish a deeper connection between number theory and complex analysis.
Furthermore, the Riemann Hypothesis has connections to various areas of mathematics and science, including cryptography, quantum mechanics, and the distribution of zeros of other L-functions. The Riemann zeta function and its generalizations play a central role in the study of analytic number theory and have applications in fields ranging from physics to computer science.
Current Status
Despite extensive study and numerous attempts at proof, the Riemann Hypothesis remains unproven. The Riemann zeta function and its properties continue to fascinate mathematicians and inspire research into the nature of prime numbers and the distribution of zeros of L-functions.
Mathematicians have made significant progress in understanding the distribution of prime numbers and the behavior of the Riemann zeta function, but the proof of the Riemann Hypothesis remains one of the most elusive and challenging problems in mathematics.
Conclusion
The Riemann Hypothesis is a central problem in mathematics that has captivated the imaginations of mathematicians for over a century. With its deep connections to number theory, complex analysis, and various areas of mathematics and science, the Riemann Hypothesis represents a profound and enduring challenge that continues to inspire research and exploration.
As mathematicians continue to explore the Riemann Hypothesis and its implications, they uncover new insights into the nature of prime numbers, the structure of the number system, and the connections between different areas of mathematics and science. Whether the Riemann Hypothesis is ultimately proven true or false, its legacy will endure as a testament to the power of mathematical inquiry and the pursuit of knowledge.