The Mathematics of Networks
Networks are ubiquitous in modern society, playing a central role in areas such as communication, transportation, social interaction.
published : 26 March 2024
Networks are ubiquitous in modern society, playing a central role in areas such as communication, transportation, social interaction, and information exchange. The mathematics of networks provides powerful tools and techniques for analyzing the structure, behavior, and dynamics of complex networks, enabling us to understand their properties and optimize their performance.
Graph Theory
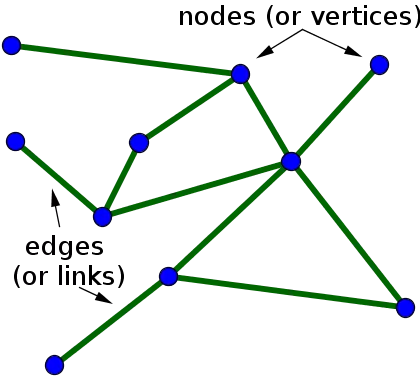
Graph theory is the branch of mathematics that studies the properties of graphs, which are mathematical structures that represent relationships between objects. A graph consists of vertices (nodes) and edges (links) that connect pairs of vertices. Graph theory provides a framework for modeling and analyzing the structure of networks and studying their properties.
Graph-theoretic concepts such as degree distribution, clustering coefficient, and centrality measures are used to characterize the structure of networks and quantify their properties. By analyzing the topology of networks and identifying key features such as hubs, clusters, and communities, researchers can gain insights into the organization and behavior of complex systems.
Network Dynamics
Network dynamics focuses on the study of how networks evolve over time and how their structure and behavior change in response to external factors and internal processes. Dynamic models such as random walks, diffusion processes, and epidemic models are used to simulate the spread of information, influence, or diseases on networks.
Understanding the dynamics of networks is essential for predicting their behavior, optimizing their performance, and designing strategies for controlling or influencing their evolution. By studying how information, influence, or pathogens propagate through networks, researchers can develop interventions and policies to promote positive outcomes or mitigate negative consequences.
Applications of Network Theory
The mathematics of networks has applications in a wide range of fields, including social networks, transportation networks, communication networks, biological networks, and information networks. In social networks, for example, graph theory is used to analyze the structure of social connections and identify influential individuals or communities.
In transportation networks, network optimization techniques are used to design efficient routes and schedules, minimize congestion, and improve the reliability and resilience of transportation systems. In communication networks, graph algorithms are used to route data packets, allocate resources, and optimize network performance.
Conclusion
The mathematics of networks provides a powerful framework for analyzing the structure, behavior, and dynamics of complex systems. By applying mathematical tools and techniques from graph theory, network theory, and dynamic modeling, researchers can gain insights into the properties and behaviors of networks and develop strategies for optimizing their performance and resilience.
As we continue to rely on networks for communication, transportation, and information exchange, the mathematics of networks will play an increasingly important role in understanding and managing the complex systems that underpin modern society. By embracing network theory and applying mathematical techniques to real-world problems, we can harness the power of networks to create more efficient, resilient, and interconnected systems for the benefit of all.