How mathematics can help us understand tumor growth

In our daily life, we unfortunately have become used to seeing images of tumors and melanomas.

published : 11 April 2024

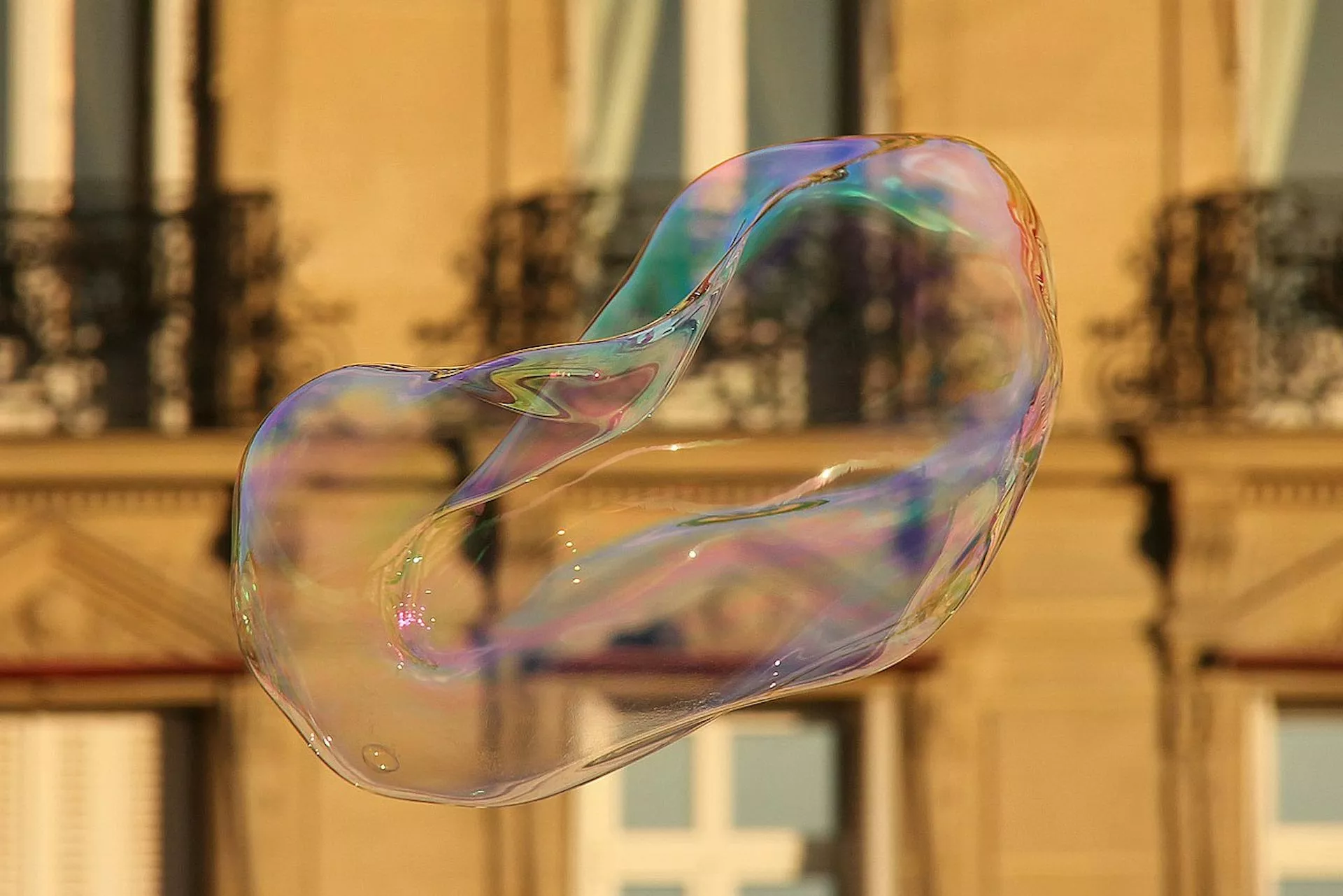
In our daily life, we unfortunately have become used to seeing images of tumors and melanomas. You may have noticed that they’re are not entirely symmetric. This asymmetry is useful to doctors in their diagnoses, but why are they asymmetric?

Instinctively, we think that symmetric objects are most often found in nature, but perhaps assymetry is even more common. To complicate things, the same object may sometimes be symmetric and sometimes not. Take soap bubbles for example. When they are small, they seem perfectly symmetric, but when we increase their radius, we see that symmetry is broken: the soap bubble is not perfectly round anymore. This phenomenon is due to the presence of physical effects such as wind and gravity. Therefore, we may affirm that the final shape of the soap bubble is caused by several factors, and the effect of each of those cannot be ignored.

The same happens for cancer growth: the asymmetric shape is due to different biological phenomena. To understand what those phenomena are is still at the center of ongoing research in biology and medicine. Mathematics may give a valuable insight on different aspects of tumor growth. By constructing mathematical models and investigating their solutions, we distinguish between various possible aspects in the mechanisms of tumor growth. This may be useful in developing effective treatments and providing biologists and doctors with complementary information.

Can we model how a tumor grows?

The shape of a tumor is the result of several interactions between tumor cells, healthy cells, molecules and other tissues. To mathematically describe its evolution from a global point of view, one can use a “diffusion equation”. Diffusion equations are good mathematical tools in such a context because they allow to describe the global effects of a physical process which takes place on a much smaller scale.

In general, the process at small scale is diffusion: a net movement of any object (for instance atoms or molecules) from a region of high concentration to a region of lower concentration. One example of such behavior can be the evolution of the temperature (or heat) in a room. We know, by experience, that if we heat one small part of our room, soon the heat will spread over to the rest of it. Nowadays we know that this thermal equilibrium is reached because the atoms and molecules composing the air are moving randomly and disorderly. This motion, called Brownian motion, is named after Robert Brown, an English botanist who first described it in 1827 while observing the movement of pollen particles in water. Interestingly, diffusion equations in mathematics were already studied independently since 1822, when Joseph Fourier introduced his landmark heat equation.

However, the connection between the small scale (Brownian motion) and the global effect of thermal equilibrium was only pointed out by Albert Einstein and Marian Smoluchowski in 1905.

Different types of diffusion and different models

Einstein described a particular type of diffusion, nowadays called the “linear diffusion”. It is characterized by its “mean squared displacement”, an average of how much the particles move in time. The “mean squared displacement” is linear in time, meaning that, on average, if we wait 5 units in time, the particles will move of √5 units in space. The linearity here is between the quantity of time and the square of the quantity of space.

This is not the only possible diffusion and other types have been used and studied, their classification often depending on this notion of “mean squared displacement”. For instance, in the “superdiffusion”, the particles are allowed to “make jumps” (nowadays called Lévy walks) and so to move more in space. This behavior is not only common for molecules but has been observed in animals. For example, it describes well the the foraging strategies of an Albatros. We may notice the differences between the trajectories of a Brownian motion and those of the albatros. In the former the particle stays close to its initial position while in the latter the albatros makes long movements (Lévy jumps).

One of the main advantages in mathematics is that, often, similar techniques and concepts can be adapted to describe different situations in nature. This is the case of parabolic equations, which are a generalization of the above diffusion equations, and are used to model a big variety of phenomena such as the oscillation of prices of the stock market or the evolution of a material undergoing a phase transition, for example the melting of ice into water. The common feature in the phenomena described by parabolic equations is always the description of a global effect arising from a process on a smaller scale.

The shape of a tumor

Assuming that every cell is (more or less) moving randomly we may describe the evolution of the cell density in space (number of cells per volume unit) by a diffusion equation. However, we will not obtain an asymmetric evolution by considering only the cell density. Indeed, a feature of diffusion equations is exactly to make the evolution more symmetric, in an effect similar to the thermal equilibrium explained above.

To obtain asymmetries, we need more elements in the model, but which effect has to be added? This is when mathematics can be useful to biology as we mathematicians can test hypotheses. Indeed, by adding different elements to the model, we can simulate different aspects of the tumor growth and better understand its mechanisms. Such elements may be, for instance, the presence of nutrient (generally oxygen or glucose brought by blood vessels), which presence is again modeled by a diffusion equation describing how the tumor consumes the nutrients, or the presence of an external pressure applied by other tissues, for example an organ by one side of a tumor. By including these features in the model, we can obtain shapes as those in the above figure, closer to what we see in the real world.