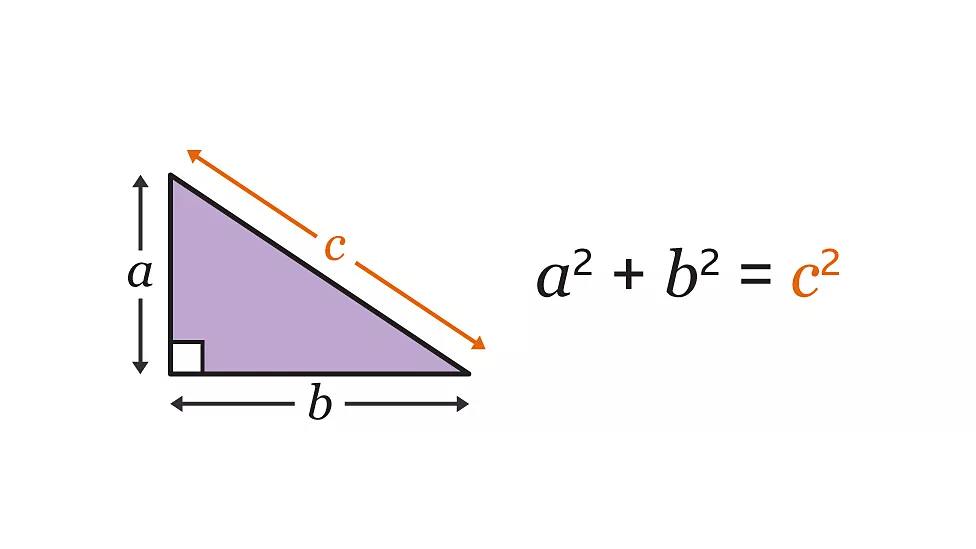Adventures in Algebra
the branch of mathematics that deals with symbols and the rules
published : 10 April 2024

Algebra, the branch of mathematics that deals with symbols and the rules for manipulating those symbols, is often considered a gateway to higher mathematics. Its concepts underpin various fields, from engineering to finance, making it a crucial area of study for students and professionals alike.
The Foundations of Algebra
At its core, algebra explores relationships between quantities using letters and symbols to represent unknown variables. It encompasses a wide range of topics, including equations, inequalities, functions, and polynomials.
One of the fundamental concepts in algebra is the equation. An equation is a mathematical statement that asserts the equality of two expressions. Solving equations involves finding the values of the variables that make the equation true. This process often requires applying various algebraic techniques, such as factoring, completing the square, or using the quadratic formula.
Inequalities, on the other hand, express relationships between quantities that are not necessarily equal. Solving inequalities involves determining the possible values of the variables that satisfy the given conditions. These concepts find applications in areas such as optimization problems and decision-making processes.
Exploring Algebraic Structures
Beyond equations and inequalities, algebra delves into the study of algebraic structures, such as groups, rings, and fields. These abstract mathematical objects provide a framework for understanding symmetry, transformations, and the properties of mathematical operations.
A group, for example, is a set equipped with a binary operation that satisfies certain axioms, such as closure, associativity, identity, and invertibility. Groups arise naturally in various contexts, including symmetries of geometric figures, permutations, and transformations.
Rings and fields extend the concept of groups by introducing additional algebraic structures and operations. Rings generalize the arithmetic of integers, while fields further extend the concept to include division.
Applications of Algebra
Algebraic techniques have widespread applications across diverse fields. In physics, algebra is used to formulate mathematical models describing the behavior of physical systems, from classical mechanics to quantum theory.
In engineering, algebra plays a central role in designing and analyzing systems, ranging from electrical circuits to structural mechanics. It provides tools for solving complex problems and optimizing designs.
Finance and economics rely heavily on algebraic concepts, particularly in the analysis of financial markets, risk management, and optimization of investment strategies. Algebraic models help forecast trends, evaluate investments, and mitigate risks.
The Future of Algebra
As technology continues to advance, algebra remains a vital component of mathematical literacy. With the increasing prevalence of data-driven decision-making and artificial intelligence, the ability to understand and manipulate algebraic expressions is more important than ever.
Moreover, algebra serves as a foundation for more advanced mathematical disciplines, such as calculus, linear algebra, and abstract algebra. Mastery of algebraic techniques opens doors to deeper insights into the structure of mathematics and its applications.
Ultimately, the adventures in algebra are not merely about solving equations or manipulating symbols but about exploring the interconnectedness of mathematical concepts and their real-world implications. Whether unraveling the mysteries of the universe or optimizing everyday processes, algebra offers a pathway to discovery and innovation.