Mathematical Marvels: From Pythagoras to Present
the universal language of the sciences, has captivated human minds for millennia. From ancient civilizations to modern societies
published : 06 April 2024
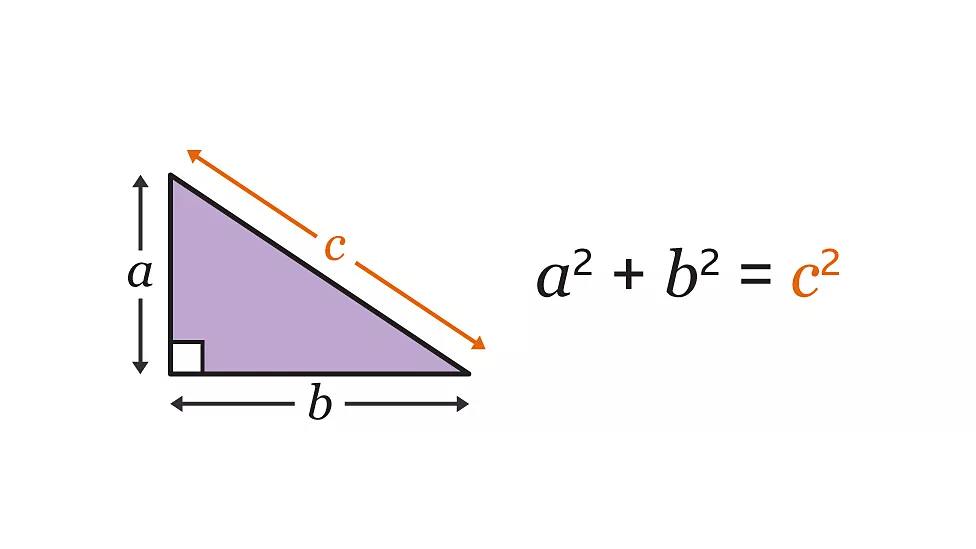
Mathematics, the universal language of the sciences, has captivated human minds for millennia. From ancient civilizations to modern societies, mathematicians have explored the depths of number theory, geometry, algebra, and calculus, unraveling the mysteries of the universe and pushing the boundaries of human knowledge.
The Legacy of Pythagoras
One of the earliest mathematical marvels is attributed to the ancient Greek mathematician Pythagoras, who is best known for the Pythagorean theorem. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
The Pythagorean theorem has far-reaching implications in mathematics, physics, engineering, and beyond. It forms the basis for trigonometry, enabling the calculation of distances, angles, and velocities in various contexts.
The Golden Ratio and Fibonacci Sequence
Another mathematical marvel is the golden ratio, a special number approximately equal to 1.618033988749895. This ratio appears in various natural and geometric contexts, from the proportions of the human body to the spirals of seashells and the growth patterns of plants.
Related to the golden ratio is the Fibonacci sequence, a series of numbers in which each number is the sum of the two preceding ones (0, 1, 1, 2, 3, 5, 8, 13, ...). This sequence appears in nature, art, and architecture, reflecting underlying patterns of growth and symmetry.
The Beauty of Fractals
Fractals, intricate geometric patterns that repeat at every scale, represent another mathematical marvel. Discovered in the 20th century, fractals offer a visual representation of complex systems and natural phenomena, from the branching patterns of trees to the contours of coastlines.
Fractal geometry has applications in computer graphics, art, physics, and biology, providing insights into the underlying structures of natural and artificial systems.
The Revolution of Calculus
Calculus, developed independently by Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century, revolutionized mathematics and science. Calculus provides a framework for understanding rates of change, accumulations, and continuous processes.
Key concepts in calculus include derivatives, which represent rates of change, and integrals, which represent accumulated change. These concepts have applications in physics, engineering, economics, and many other fields.
Modern Marvels and Future Frontiers
Modern mathematics continues to push the boundaries of human understanding, with discoveries in fields such as topology, number theory, and cryptography. Mathematicians explore the nature of infinity, the structure of high-dimensional spaces, and the properties of prime numbers.
Moreover, mathematics plays a crucial role in shaping the technologies of the future, from artificial intelligence and machine learning to quantum computing and cryptography. As society becomes increasingly reliant on data-driven decision-making and advanced technologies, the importance of mathematics in solving complex problems and driving innovation has never been greater.
Conclusion
From ancient civilizations to modern societies, mathematics has been a driving force behind human progress and innovation. The marvels of mathematics—from the Pythagorean theorem to fractals and calculus—reveal the beauty, elegance, and power of the mathematical universe.
As we continue our journey into the world of mathematics, let us marvel at the wonders that have been uncovered and the mysteries that await discovery. For in the realm of mathematics, the possibilities are infinite, and the beauty is eternal.